Rational Numbers: A rational number is a number which can be expressed in the form of p/q where p and q are and is not zero. It is denoted by Q.

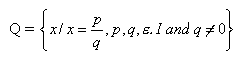
Properties Law for Addition:

a) Commutative Law for addition:

A +b = b+ a a, b ε Q

b) Associative Law for addition:

                                    (a+b)+c=a+ (b+c) a, b, c ε Q

c) Additive Identity:

The rational number O is such that

                                    A + O = O + a = a a ε Q

d) Additive inverse:

            To each a ε Q. there is a number – a ε Q i.e.

                                     a + (-a) = (-a) + a=0

e) Commutative Law for Multiplication:

                                    a .b = b .a a, b ε Q

f) Associative Law for Multiplication:

                                    (a .b). c = a .(b .c)  a, b c ε Q

g) Multiplicative identity:

            The rational number 1 (unity), is such that

                                    1 .a = a .1 = a  a ε Q

h) Multiplicative Inverse:

            To every non-zero a ε Q. there corresponds a rational numbers such such that a. .

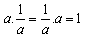
i) Distributive Law:

            For a, b, c, ε Q

            a. (b+c) =a .b+a.c. and (a+b). c=a.c+b.c

Top